The world of fluid inclusions

CO₂ is a major component of natural fluids particularly in metamorphic and high grade metamorphic rocks.

Generally speaking CO₂ is mixed with water but can also be found as a pure component in some geological contexts.

The inclusion used in the video come from a xenolith sampled in the Amelaco volcano (Mexico). Secondary inclusions were found in plagioclase crystals.

They are essentially composed of pure CO₂ ( Aguirre-Diaz et al., 2002^[1]).

The video starts at a temperature of 14.7°C. At this temperature the inclusion presents two phases, a liquid and a vapour phase. The first part of the video is cooling.

During cooling the only visible change is the regular increase of the vapour bubble size.

At about -96°C a drastic change of the inclusion content occurs: This is the sudden crystallization of solid CO₂. The phase transition is therefore: Liquid CO₂ → solid CO₂.

During heating the aspect of solid CO₂ continuously changes, probably related to recrystallization or re-organization of the solid phase.

At precisely -56.6°C solid CO₂ sharply melts. This is the melting of CO₂.

Continuing heating only modifies progressively the vapour bubble by decreasing the size up to about 15°C. Thus the bubble size is very small and the vapour phase begins to move rapidly – this is the Brownian motion. The bubble moves more and more rapidly as the diameter decreases.

At the temperature of 17.8°C the bubble, reduced as a single point, completely disappears. This is homogenization [see page dedicated to homogenization into the liquid phase].

At room temperature this inclusion is monophase.

At 17.8°C the bubble disappears. This transition is called homogenization. It corresponds to the transition: liquid CO₂ → vapour CO₂. The inclusion is now monophase.

No change occurs up to room temperature.

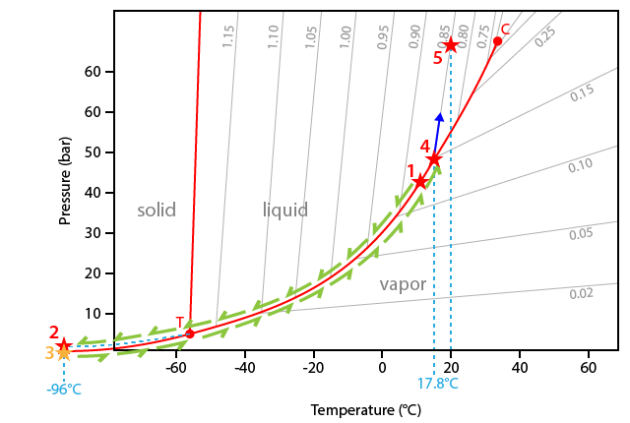
The interpretation of the sequence will be made in the CO₂ phase system. This diagram is very similar with that of pure H₂O, but differs by the negative slope of the melting curve and the position of the invariant point (critical point at 31.1°C and triple point at -56.6°C).

The experiment starts at 14.7°C. At this temperature the inclusion contains two phases (liquid+vapour) and the representative point of the inclusions is therefore located on the liquid+vapour curve (point #1).

During cooling, the inclusion follows the liquid+vapour curve down to the triple point (point T). The predicted crystallization of solid CO₂ does not occur because of metastability reasons. The inclusion therefore goes on cooling along a metastable extension of the liquid+vapour curve down to about -96°C (point #2).

The carbonic liquid of the inclusion thus crystallizes and the inclusion drops down to the sublimation curve (solid+vapour) (point #3).

During heating the temperature-pressure path of the inclusion follows the sublimation curve up to the triple point (point T).

At the triple point T, solid CO₂ suddenly melts to liquid CO₂ (temperature of -56.6°C).

Furthermore the inclusion follows the liquid-vapour curve. The following phase transition is the disappearance of the vapour bubble at a temperature of 17.8°C.

At this temperature (point #4) the inclusion leaves the liquid+vapour curve. Note that the internal pressure inside the inclusion if about 45 bar, that is 45 times the atmospheric pressure!

Going on heating, the inclusion begins to climb along its isochore. The isochore corresponds to a temperature-pressure line of constant density. In the present case the corresponding density is 0.85 g.cm^-3.

No other change is observed up to room temperature (point #5).

The density of CO₂ can be calculated using the mathematical expression of Parry (1986)^[2]:

• if homogenization occurs into the liquid phase (disappearance of the vapour phase);

  \(\left(\frac{d_{CO_2}}{dc_{CO_2}}-1\right)=C_0\left(1-\frac{T}{T_c}\right)^{0,347}+\displaystyle{\sum_{i=1}^2 C_i\left(1-\frac{T}{T_c}\right)^{(i+1)/3}}\)

• if homogenization occurs into the vapour phase (disappearance of the liquid phase);

  \(\left(\frac{d_{CO_2}}{dc_{CO_2}}-1\right)=D_0\left(1-\frac{T}{T_c}\right)^{0,347}+\displaystyle{\sum_{i=1}^2 D_i\left(1-\frac{T}{T_c}\right)^{(i+1)/3}}\)

• \(T\) is the CO₂ melting temperature (in K), \(T\)_c is the critical temperature of CO₂ (304.21 K) and \(dc_{CO_2}\) is the critical density of CO₂ (0.01059 g.cm³). The coefficients C_i and D_i take the following values:

\(\begin{array}{cccc}C_0=&1,9073793&D_0=&-1,7988929\\C_1=&0,38225012&D_1=&-0,71728276\\C_2=&0,42897885&D_2=&1,7739244\end{array}\)

Pure CO₂-bearing fluid inclusions are generally found in high-grade metamorphic rocks, notably in granulitic environments ( Touret, 2001^[3]). Indeed fluids of the lower crust seem to be dominated by CO₂.

In addition fluids composed of pure CO₂ can be also found in rocks of mantle origin. CO₂ can also be produced during a boiling process close to a magmatic chamber.

Finally post-trapping phenonema such as leakage of water out of cavities can result in the production of pure CO₂-bearing inclusions ( Bakker and Janssen 1991^[4]), such as in mesothermal gold lode deposits of the West African craton ( Schmidt Mumm et al., 1997^[5]).